Rumus Fluida Statis Fisika Kelas XI semester 2

A. Hukum Archimedes



ketika benda tercelup seluruhnya tekanan hidrostatis dialami permukaan bagian atas dengan luas area A, sebesar P1 dan bagian bawah sebesar P2. Dengan demikian gaya ke atas dapat kita tentukan sebgai berikut:

Ket: Fa= gaya ke  atas (N) ; r = massa jenis fluida (kg/m³);  g = percepatan gravitasi (m/s²); V_t = Volume benda yang tercelup/volum fluida yang dipindahkan.

Dengan demikian sebuah benda yang tercelup seluruhnya atau sebagian dalam suatu fluida akan mendapat gaya ke atas oleh sebuah gaya sama besar dengan berat fluida yang dipindahkan.  Pernyataan ini disebut dengan Hukum Archimedes.

Analisis perbandingan massa jenis benda dengan massa jenis fluida ketika benda di dalam zat cair

Dari ketiga peristiwa tersebut, dapatlah kita simpulkan bahwa suatu benda akan tenggelam tinggal dilihat dari kerapatan benda/massa jenis bendanya dibandingkan dengan massa jenis fluida. Pada gambar diatas orang tersebut terapung di atas air laut mati, karena massa jenis orang tersebut jauh lebih kecil dari massa jenis air laut mati.

Begitu juga kapal yang begitu besar massanya dapat terapung, karena dengan rumus rho=m/V, dengan memperbesar volume kapal kita harapkan massa jenis kapalnya menjadi lebih kecil dari massa jenis air laut. Dengan ilmu ini juga manusia teelah mampu menciptakan kapal terapung juga kapal selam.

B. Tekanan Hidrostatis

Hukum Utama Hidrostatis- Sebelumnya telah dibahas mengenai pengertian tekanan hirostatis sekarang perhatikanlah bejana berhubungan pada Gambar 7.7. Gambar tersebut memperlihatkan sebuah bejana berhubungan yang diisi dengan fluida, misalnya air. Anda dapat melihat bahwa tinggi permukaan air di setiap tabung adalah sama, walaupun bentuk setiap tabung berbeda. Bagaimanakah tekanan yang dialami oleh suatu titik di setiap tabung? Samakah tekanan total di titik A, B, C, dan D yang letaknya segaris? Untuk menjawab pertanyaan tersebut, Anda harus mengetahui Hukum Utama Hidrostatis.

Gambar 7.7 Tekanan di titik A, B, C, dan D sama besar, serta tidak bergantung pada bentuk penampang tempat fluida tersebut.

Hukum Utama Hidrostatis menyatakan bahwa semua titik yang berada pada bidang datar yang sama dalam fluida homogen, memiliki tekanan total yang sama. Jadi, walaupun bentuk penampang tabung berbeda, besarnya tekanan total di titik A, B, C, dan D adalah sama. Persamaan Hukum Utama Hidrostatis dapat diturunkan dengan memperhatikan Gambar 7.8. Misalkan, pada suatu bejana berhubungan dimasukkan dua jenis fluida yang massa jenisnya berbeda, yaitu ρ 1 dan ρ 2.

Gambar 7.8 Tekanan total di titik A dan B pada bejana U yang terisi fluida homogen adalah sama besar, pA = pB.

Jika diukur dari bidang batas terendah antara fluida 1 dan fluida 2, yaitu titik B dan titik A, fluida 2 memiliki ketinggian h₂ dan fluida 1 memiliki ketinggian h₁. Tekanan total di titik A dan titik B sama besar. Menurut persamaan tekanan hidrostatis, besarnya tekanan di titik A dan titik B bergantung pada massa jenis fluida dan ketinggian fluida di dalam tabung. Secara matematis, persamaannya dapat dituliskan sebagai berikut.

p_A = p_B
p₀ + ρ₁gh₁ = p0 + ρ₂gh₂
ρ₁ h₁ = ρ₂ h₂
dengan: h₁ = jarak titik A terhadap permukaan fluida 1,
h₂ = jarak titik B terhadap permukaan fluida 2,
ρ₁ = massa jenis fluida satu, dan
ρ₂ = massa jenis fluida dua.
Contoh menghitung tekanan pada pipa U

Perhatikanlah gambar bejana di samping Jika diketahui massa jenis minyak 0,8 g/cm³, massa jenis raksa 13,6 g/cm³, dan massa jenis air 1 g/cm³, tentukanlah perbedaan tinggi permukaan antara minyak dan air.

Jawab
Diketahui: ρ m = 0,8 g/cm³, ρ r = 13,6, dan ρ air = 1 g/cm³.
Air dan minyak batas terendahnya sama sehingga diperoleh persamaan berikut
ρ_a h_a = ρ_m h_m

Jadi, perbedaan tinggi permukaan minyak dan air = 15 cm – 12 cm = 3 cm.

C. Hukum Pascal

Hukum ini menyatakan bahwa 

Perubahan tekanan pada setiap titik dalam fluida tertutup disebarkan sama pada seluruh cairan ke segala arah.

Dongkrak Hidrolik: Dongkrak digunakan untuk mengangkat mobil yang akan dicuci menggunakan hukum pascal. Seperti yang terlihat pada gambar dibawah ini. Saat kita mendorong salah satu piston dengan gaya f maka fluida didalamnya tertekan kemudian menyebarkan tekanan dengan merata ke segala arah, sehingga mampu menekan piston lain yang ditumpangi mobil yang kemudian terangkat.

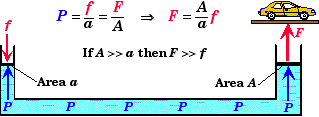gambar: faculty.wwu.edu

Begitupun dengan suntikan, kita memberikan tekanan pada salah satu ujung suntikan kemudian cairan keluar melalui ujung tajam jarum suntikan tersebut. Masih banyak contoh lainnya.

Rumus Hukum Pascal
Semua contoh penerapan diatas memenuhi persamaan hukum pascal sebagai berikut:

P1 = P2
F1/A1 = F2/A2

Keterangan:

P = Tekanan (Pascal)

F = Gaya (N)

A = Luas Permukaan (m*2)

* Suntikan memiliki luar penampang/permukaan lingkaran

Contoh Soal:

Alat pengangkat mobil yang memiliki luas pengisap masing-masing sebesar 0,10 m² dan 2 × 10^–4 m² digunakan untuk mengangkat mobil seberat 10⁴ N. Berapakah besar gaya yang harus diberikan pada pengisap yang kecil? 

Jawab:

F1/A1 = F2/A2  

10⁴/0,1 = F1/2 × 10^–4

^{100.000 = F1/2 × 10–4}

^{F1 = 20 N}

Sumber: http://fisika79.wordpress.com/tag/hukum-archimedes/

             http://budisma.web.id/materi/sma/fisika-kelas-xi/hukum-utama-hidrostatis/

             http://www.gomuda.com/2013/01/fluida-statis-hukum-pascal.html

Posted in: Fisika,Pelajaran,tugas